Paging

Till now we have seen that an \(n\) bit CPU would imply that there are \(2^n\) addressible locations and with byte addressible 64-bit systems that amounts to 16 exabytes !!

Fyi, Google data centers have 27 petabytes of storage!

We therefore use virtual memory. Memory in our programs is #virtual, in the sense that we can assume that the total available memory is \(2^{64}\)(or\(2^{32}\)). Typically the picture that we would have in mind is the following:

alt text

Also, we want to run various programs (including our dear OS) at once, keeping data and code separate is exteremley important to ensure functional correctness.

One solution could be allocating disjoint segments of memory to every program and keep track of the "address space (program's section of memory)" associated with every process.

Typically the programs we would write are of KBs and some MBs of stack might be allocated, but allocating \(2^{32}\) bytes for every program is an overkill + infeasible.

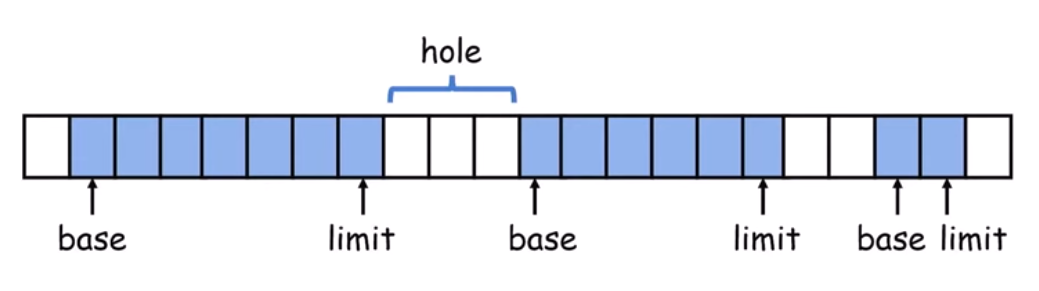
Another solution could be allocating space dynamically to programs like the following: alt text

Issues with this scheme is we need to know before hand how much space a program occupies and then find a hole (empty space in memory) than can accomodate our process. It is possible that any given hole might not be able to accomodate the program, but the total space occupied by the holes over the memory might be sufficient.

Above all this makes programming difficult and we are proud lazy engineers!

The solution to above problems is using virtual memory and paging.

Virtual memory: The programmer assumes that the address space of the program is \(2^n\) bytes wide for n-bit systems. The adress starts at 0x0.

Paging: The main memory is divided into chunks typically of 4KBs called pages.

How does paging work?

The adresses generated by the CPU contain virtual address. These are specified by the programmer. To actually access the Data from the RAM, we need a translator in hardware (see figure)

alt text

The virtual address space of the process is divided into pages. 4KB = \(2^{12}\) bytes and therefore \(2^{12}\) bytes are grouped together in pages. Assume we have a 32 bit system. Thus, the VA contains \(2^{20}\) virtual pages. Each page needs to be mapped a physical page (aka frame) in the RAM, and this translation is done in the hardware using a page table

alt text

Pages in main memory need not remain contiguous.

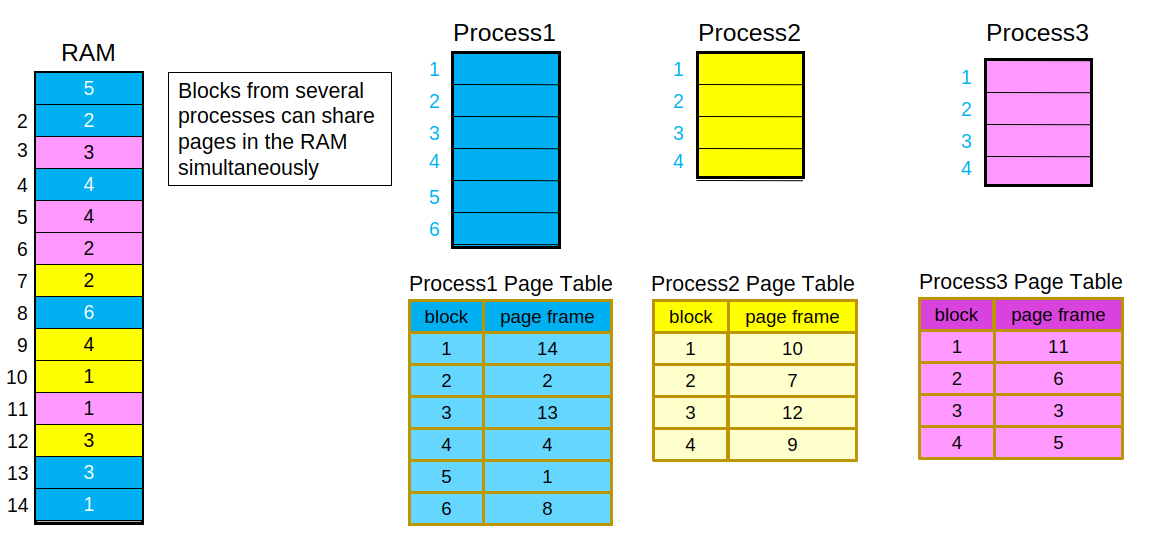
alt text

Main memory (DRAM) is a very small space. We typically have SSDs that meant only for storage, and most of our programs are stored there. In order to run a program we need to load text section in main memory.

  • When all pages are not needed, we can do demand paging i.e., load only those pages which are required, into the main memory and write their translations to the page table.

  • A present bit has to be stored with every translation to check if the page we are asking for is there in main memory.

  • Since main memory is limited, if another page for a process has to be loaded, we need to replace a page. If the page was not changed, we can discard it, since its copy sits in the disk already, otherwise we need to update the copy in the disk with the changed version of the replaced page.

  • A dirty bit has to be maintained to check if a given page was changed after loading into memory.

What exaclty is happening?

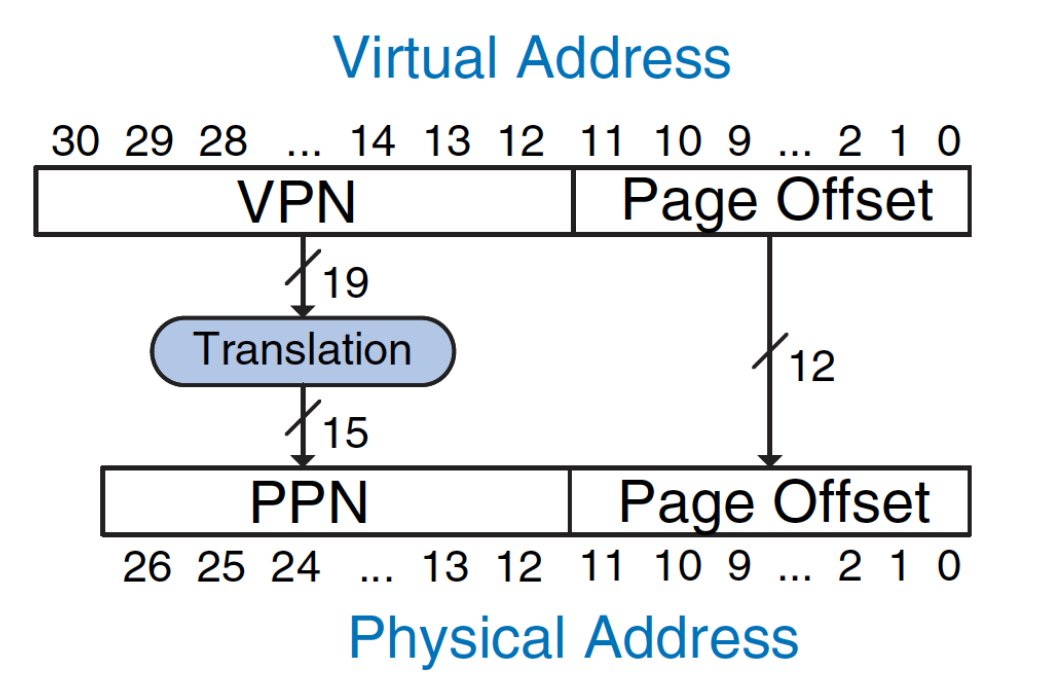
Consider the instruction ld x1, 0(x2) the user has set up some address in x2 which is virtual and wants to load the value into register x1. Assuming 32 bit addresses, the first 20 bits are passed into the page table, and the physical page number is found.

Note that:

  • the page table is indexed using virtual page number (first 20 bits)
  • the PPN (frame number) is essentially the physical address of the 0th entry of that frame.
  • the offset inside the page doesnt change in translation.

After getting the PPN, the address to be accessed is PPN + offset(12). The physical address is accessed and the value stored is loaded into x1.

alt text

// more content ...

References